Binary Search 이분탐색
Binary search
이분탐색
이분 탐색은 정렬된 배열에서 원하는 값이 어디에 있는지 빠르게 찾아내는 방법이다.
탐색의 유명한 예로 사전을 들 수가 있다. 사전의 경우, 색인이 있어서 가나다 순이라던가, 주제별로 묶여있어서 우리가 원하는 것을 색인을 통해 찾기도 한다. 하지만 이러한 색인이 없다면, 무지성으로 처음부터 끝까지 한장씩 찾아보는 수 밖에 없다. 하지만, 데이터가 정렬되어 있다면 이분탐색을 통해 어디에 있는지 빠르게 찾을 수 있다.
문제를 푸는 핵심은 정렬 후, 우리가 원하는 값이 현재 기준(mid)보다 큰지 작은지를 확인하여, 탐색범위를 점차적으로 줄이는 원리를 이해하는 것이다.
이분 탐색을 소개할때 자주 쓰이는 것이 UP and DOWN인데, 이를 생각하면서 읽으면 좋을 것이다.
주요 포인트는 범위를 left, right라는 변수로 잡고, 그 중간 값인 mid(left+right/2)를 통해 mid가 우리가 찾는 값인지 체크하는 것이다. 만약 mid가 우리가 찾는 값보다 작으면 right의 범위를 이동하여, 다음 턴에 left~mid에서 찾고, mid가 찾는 값보다 크면 left를 mid로 범위를 설정해서 다시 탐색하는 방식이다.
아래와 같이 -1 ~ 19까지 정렬된 배열이 있다고 보자. 우리가 4라는 값이 어디있는지 찾으려면 이진 탐색을 이용해 다음과 같은 과정을 가진다. 우선 찾는 범위는 left, right 로 잡으며, 현재 비교할 값은 mid 로 지정한다.
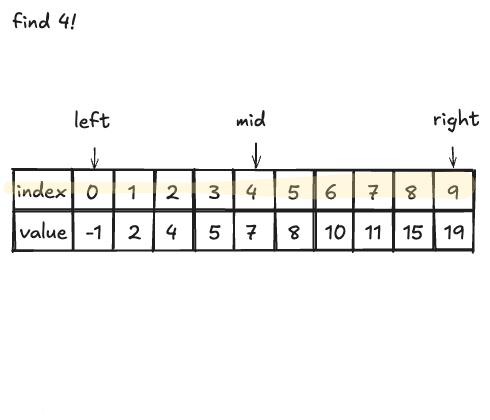
left = -1 , mid = 7, right = 19
여기서 우리가 찾는 4는 현재 mid 값인 7보다 작기 때문에 범위를 left와 mid로 다시 잡고 찾아야 한다.
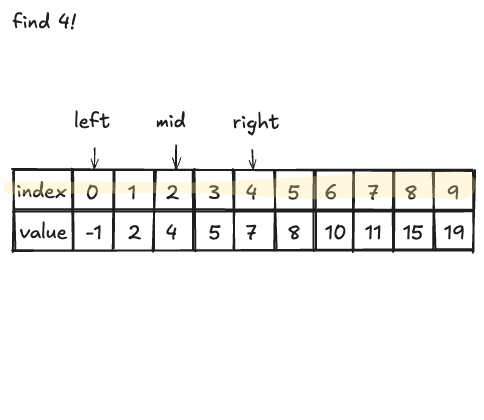
left = -1 , mid = 4, right = 7
다시 범위를 잡으면, mid의 값이 우리가 찾는 4와 동일하다. 여기까지 하면, 우리가 찾는 값이 index 2에 있는 것을 알 수 있다. 이처럼 우리가 찾는 값인지 확인하려면 배열을 처음부터 끝까지 10번 연산하여 찾을 수도 있지만, 이진 탐색을 이용하면 약 2번만에 우리가 원하는 것을 찾을 수 있다.
만약 여기서 5를 찾는다고 하면 어떨까? 5는 현재 mid의 값인 4보다 크기 때문에 범위를 mid, right로 새로 잡는다.
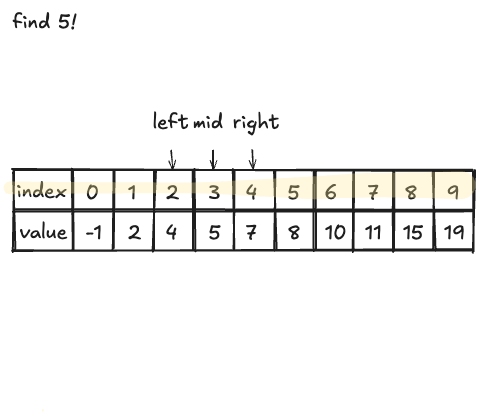
left = 4 , mid = 5, right = 7
여기서 mid 값이 우리가 찾는 값임을 확인할 수 있다.
JAVA
...
//x는 우리가 찾는 값
//d[]는 값이 들어간 배열
while(l<=r){
int mid = (l+r)/2;
if(x == d[mid]) {
System.out.println(mid);
break;
}
else if(x>d[mid]) {
l = mid+1;
}
else {
r = mid-1;
}
}
추천문제
Leave a comment