이분매칭(Bipartite Matching)

두 그룹이 있을 때, 각 그룹 노드 들이 모두 서로 다른 매칭(연결)에 속하게 만들 수 있는 그래프를 이분 그래프(Bipartite Graph) 라고 한다.

이분 매칭은 두 그룹을 이분 그래프와 같이 매칭해나가는 알고리즘이다.

주로 사람에게 일을 1개씩 부여해서 최대한 모든 사람이 일할 수 있는 방법을 찾거나, 소개팅같이 1-1로 매칭할때 최대한 모든 사람이 매칭되도록 하는 등… 결론은 두 그룹으로 나눌 수 있고, 연결(매칭)을 지을 수 있다면 이분 매칭을 통해 최대한 두 그룹을 매칭시켜줄 수 있다.

하지만, 이 역시 그래프이기 때문에 그래프와 관련된 다양한 알고리즘이 사용될 수 있다.

이분 매칭은 어떻게 이뤄지나?

이분 매칭은 몇가지 방법이 있지만, 그 중 가장 이해하기 쉬운건 DFS 를 기반으로 한다. 간단한 예시로 열형강호 문제를 기반으로 하는 경우, 현재 노드가 연결하고자 하는 다른 그룹의 노드가 이미 연결된 경우, DFS 를 통해서 기존 연결을 변경하여서 연결수를 늘릴 수 있을 지를 확인한다. 아래 그림을 확인하자.

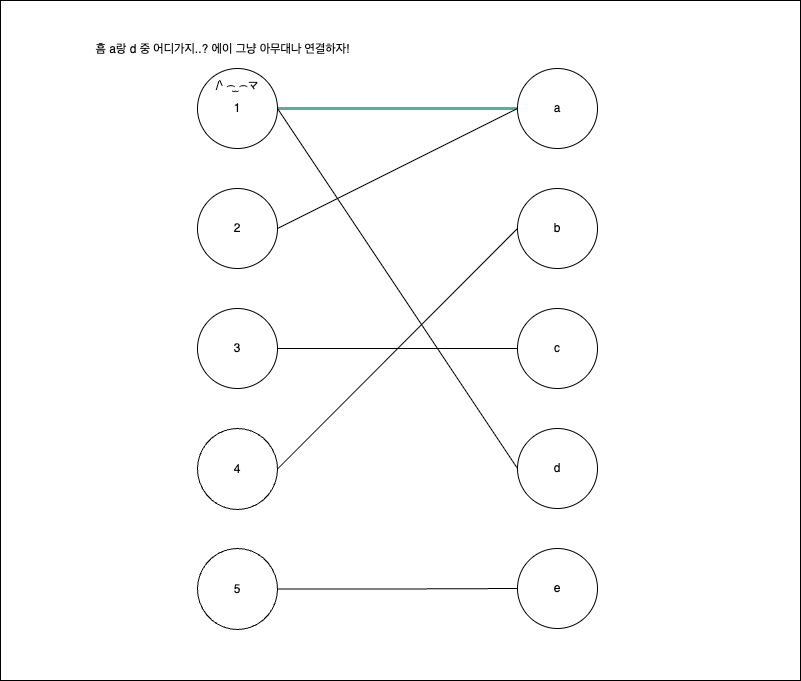
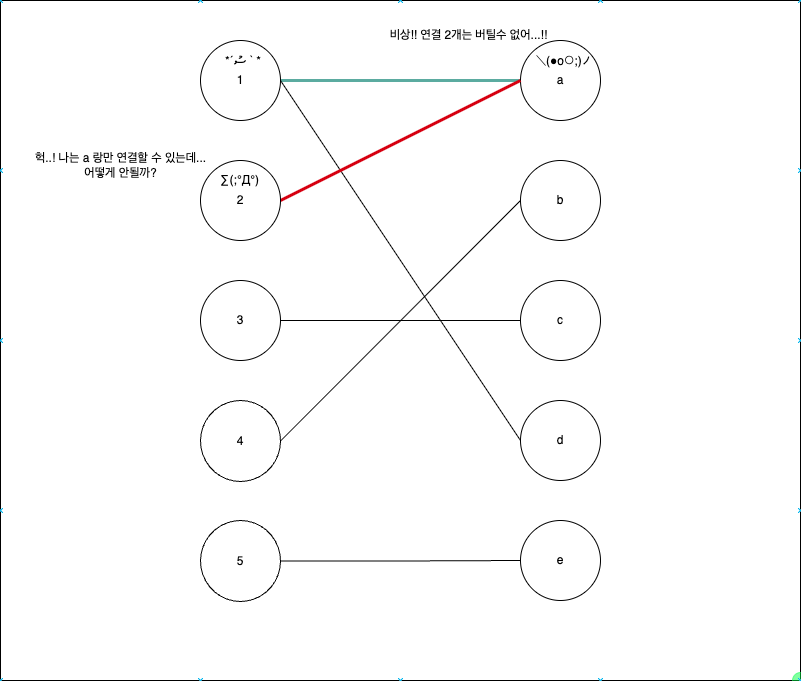
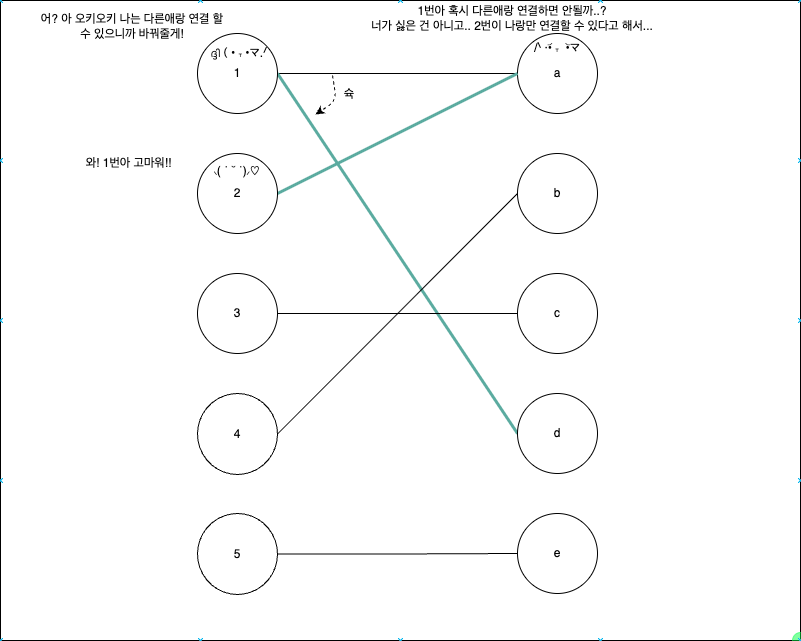
기존 목표는 두 그룹을 최대한 많이 연결을 하는 것이다. 2번 차례가 되어 연결을 하려 할 때, 기존 1-a 의 연결을 유지하는 것보다, 1의 연결을 변경하는 것이 더 좋다는 것은 직관적으로 알 수 있다. 각 노드별로 탐색하기에 시간복잡도는 아래와 같다.

시간 복잡도 : O(V*E^2)

• V : 간선(연결 수)
• E : 노드의 수 (그룹 대상의 수)

이런 일련의 과정을 DFS와 같이 보게 된다면… 최대 연결을 지으려고 할 때, 2번 → a → 1번 에게 각각 전파하면서 다른 연결을 지을 수 있는지 탐색하게 된다. 이렇게 최대 연결을 늘리는 경로를 ‘증가 경로’라고 부른다.

어어..? 잠시만요.. 뭔가.. 떠오르는 거 같기도 한데… 혹시 포드 풀커슨?!

맞다.. 위에서 말했듯이 그래프로 이뤄지기 때문에… 각 그룹에 시작점, 마지막 점을 연결하면 최대유량 문제와 동일하게 된다. 단지 각 연결의 값이 1이라는 점 빼고…! 따라서, DFS 외에 BFS 로 탐색하여 증가 경로를 찾을 수 있고, 시간복잡도를 더 줄이는 다른 방식도 있다.

포드 풀커슨, 에드몬트 카프….

// boolean[] c      //매칭 여부
// ArrayList<ArrayList<Integer>> t  //그래프
// int[] bb  //매칭된 노드 번호 저장 배열

//매칭 성공 = true return.
public static boolean dfs(int x) {
		for(int i=0; i<aa.get(x).size(); i++) {
			int t=aa.get(x).get(i);
			if(c[t]) {continue;} //이미 매칭된 경우 pass
			c[t]=true;
			//매칭될 것이 있는 경우
			if(bb[t]==0||dfs(bb[t])) {bb[t]=x; return true;}//매칭
		}
		return false;
	}

// 전체 코드

public class Main {
	
	public static boolean[] c=new boolean[202];
	public static ArrayList<ArrayList<Integer>> aa=new ArrayList<ArrayList<Integer>>();
	public static int[] bb=new int[202];

	public static boolean dfs(int x) {
		for(int i=0; i<aa.get(x).size(); i++) {
			int t=aa.get(x).get(i);
			if(c[t]) {continue;}
			c[t]=true;
			if(bb[t]==0||dfs(bb[t])) {bb[t]=x; return true;}
		}
		return false;
	}
	public static void main(String[] args) {
	 Scanner sc=new Scanner(System.in);
	 	int N=sc.nextInt(); int M=sc.nextInt();

		for(int i=0; i<=N ;i++) {
			aa.add(new ArrayList<Integer>());
		}
		for(int i=1; i<=N; i++) {
			int a=sc.nextInt();
			for(int j=0; j<a; j++) {
				int b=sc.nextInt();
				aa.get(i).add(b);
			}
		}

		int count=0;
		for(int i=1; i<=N; i++) {
			c=new boolean[202];
			if(dfs(i)) {count++;}
		}
		System.out.println(count);
	
	}
}

추천 문제

문제로는 11375: 열혈강호를 추천한다.